Next: Ocean Sciences Building Amenities. Up: PTV Operating Guidelines Previous: Compressibility of the PTV. Contents
Consider a cylinder capped on one end with an end cap and on the other end
with a piston (see Fig. 3). The cylinder
is filled with a mass, 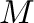 , of water which is pressurized by applying a
force,
, of water which is pressurized by applying a
force, 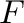 , to the piston. The force that must be applied is
, to the piston. The force that must be applied is 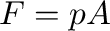 where
where
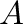 is the area of the piston and
is the area of the piston and 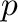 is the water pressure. The work done
in compressing the water is
is the water pressure. The work done
in compressing the water is 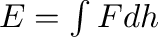 ,
,
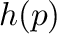 and
and 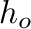 are the piston positions at pressure
are the piston positions at pressure 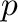 and at
atmospheric pressure, respectively. This quantity of energy is stored in
the water as potential energy and represents the maximum that might
hypothetically be converted to kinetic energy during vessel failure.
and at
atmospheric pressure, respectively. This quantity of energy is stored in
the water as potential energy and represents the maximum that might
hypothetically be converted to kinetic energy during vessel failure.
The fact that the mass of water is fixed can be used to determine the relationship between the piston position and the water pressure. Note that a fixed mass implies that
where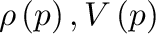 are the water density and volume
of the water at pressure,
are the water density and volume
of the water at pressure, 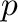 . The quantities
. The quantities 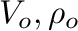 are measured at
atmospheric pressure. The dependence of water density on pressure can be
expressed as
where
are measured at
atmospheric pressure. The dependence of water density on pressure can be
expressed as
where
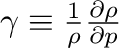 is the
compressibility of water. Table 3 demonstrates that
the compressibility is nearly constant over the range of pressures relevant
to the PTV.
is the
compressibility of water. Table 3 demonstrates that
the compressibility is nearly constant over the range of pressures relevant
to the PTV.
The density can also be expressed as
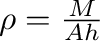 where
where 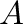 is the
cross-sectional-area of the vessel. Substituting this into (11)
yields the following equivalent relationships between the pressure and the
piston position,
is the
cross-sectional-area of the vessel. Substituting this into (11)
yields the following equivalent relationships between the pressure and the
piston position,
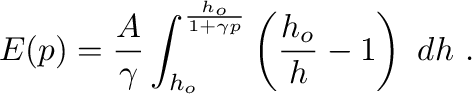 (13)
(13)
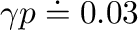 and therefore
and therefore
 . Computing the Taylor series of
(14) and neglecting third and higher order terms yields a
greatly simplified expression with an error of approximately only 3%:
. Computing the Taylor series of
(14) and neglecting third and higher order terms yields a
greatly simplified expression with an error of approximately only 3%:
Dana Swift, swift@ocean.washington.edu